Sympy#

What is Symbolic Computation?#

Symbolic computation deals with the computation of mathematical objects symbolically. This means that the mathematical objects are represented exactly, not approximately, and mathematical expressions with unevaluated variables are left in symbolic form.

Let’s take an example. Say we wanted to use the built-in Python functions to compute square roots. We might do something like this

import math

math.sqrt(9)

3.0

9 is a perfect square, so we got the exact answer, 3. But suppose we computed the square root of a number that isn’t a perfect square

math.sqrt(8)

2.8284271247461903

Here we got an approximate result. 2.82842712475 is not the exact square root of 8 (indeed, the actual square root of 8 cannot be represented by a finite decimal, since it is an irrational number). If all we cared about was the decimal form of the square root of 8, we would be done.

But suppose we want to go further. Recall that \(\sqrt{8} = \sqrt{4\cdot 2} = 2\sqrt{2}\). We would have a hard time deducing this from the above result. This is where symbolic computation comes in. With a symbolic computation system like SymPy, square roots of numbers that are not perfect squares are left unevaluated by default

import sympy

sympy.sqrt(8)
\[\displaystyle 2 \sqrt{2}\]

Why Sympy#

  1. It is free and open source, you can even use it as part of something you sell

  2. SymPy is written entirely in Python, and is executed entirely in Python. Thus it is interoperable

  3. It is very lightweight to download and install. Other packages might be Gb in size.

  4. It can be used as a library. There is an Application Programming Interface or API for use with other tools.

A more interesting example#

The above example starts to show how we can manipulate irrational numbers exactly using SymPy. But it is much more powerful than that. Symbolic computation systems (which by the way, are also often called computer algebra systems, or just CASs) such as SymPy are capable of computing symbolic expressions with variables.

Let us define a symbolic expression, representing the mathematical expression

from sympy import symbols

x, y = symbols("x y")
expr = x + 2 * y
expr
\[\displaystyle x + 2 y\]

Note that we wrote x + 2*y just as we would if x and y were ordinary Python variables. But in this case, instead of evaluating to something, the expression remains as just x + 2*y. Now let us play around with it:

expr + 1
\[\displaystyle x + 2 y + 1\]
expr - x
\[\displaystyle 2 y\]
x * expr
\[\displaystyle x \left(x + 2 y\right)\]

Notice something in the above example. When we typed expr, we did not get \(x + 2 y-x\), but rather just \(2y\). The x and the -x automatically canceled one another. This is similar to how sqrt(8) automatically turned into 2*sqrt(2) above. This isn’t always the case in SymPy, however:

from sympy import expand, factor

expanded = expand(x * expr)
expanded
\[\displaystyle x^{2} + 2 x y\]
factor(expanded)
\[\displaystyle x \left(x + 2 y\right)\]

The Power of Symbolic Computation#

  • The real power of a symbolic computation system such as SymPy is the ability to do all sorts of computations symbolically. SymPy can simplify expressions,

    • compute derivatives

    • integrals

    • limits

    • solve equations

    • work with matrices

It includes modules for plotting, printing (like 2D pretty printed output of math formulas, or \(\mathrm{\LaTeX}\), code generation, physics, statistics, combinatorics, number theory, geometry, logic, and more. Here is a small sampling of the sort of symbolic power SymPy is capable of, to whet your appetite.

# * means we import everything from the package
from sympy import *

# defines multiple symbols at once
x, t, z, nu = symbols("x t z nu")

# x is now an object of type Symbol
type(x)

sympy.core.symbol.Symbol

# This will make things look pretty
init_printing(use_unicode=True)

Class Exercise#

  1. Take the derivative of \(sin{(x)}e^x\)

  2. Compute \(\int(e^x\sin{(x)} + e^x\cos{(x)})\,dx\)

  3. Compute \(\int_{-\infty}^\infty \sin{(x^2)}\,dx\)

  4. Find \(\lim_{x\to 0}\frac{\sin{(x)}}{x}\)

  5. Solve \(x^2 - 2 = 0\)

  6. Solve the differential equation \(y'' - y = e^t\)

  1. Take the derivative of \(sin{(x)}e^x\)

# Type Your Solution Here

diff(sin(x) * exp(x), x)
../../_images/SymPy_28_0.png

  1. Compute \(\int(e^x\sin{(x)} + e^x\cos{(x)})\,dx\)

# Type Your Solution Here

integrate(exp(x) * sin(x) + exp(x) * cos(x), x)
../../_images/SymPy_31_0.png

  1. Compute \(\int_{-\infty}^\infty \sin{(x^2)}\,dx\)

# Type Your Solution Here

integrate(sin(x**2), (x, -oo, oo))
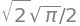
../../_images/SymPy_34_0.png

  1. Find \(\lim_{x\to 0}\frac{\sin{(x)}}{x}\)

# Type Your Solution Here

limit(sin(x) / x, x, 0)
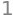
../../_images/SymPy_37_0.png

  1. Solve \(x^2 - 2 = 0\)

# Type Your Solution Here

solve(x**2 - 2, x)
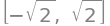
../../_images/SymPy_40_0.png

  1. Solve the differential equation \(y'' - y = e^t\)

# Type Your Solution Here

y = Function("y")
dsolve(Eq(y(t).diff(t, t) - y(t), exp(t)), y(t))
../../_images/SymPy_43_0.png

Print \(\int_{0}^{\pi} \cos^{2}{\left (x \right )}\, dx\) in \(\mathrm{\LaTeX}\)

latex(Integral(cos(x) ** 2, (x, 0, pi)))

'\\int\\limits_{0}^{\\pi} \\cos^{2}{\\left(x \\right)}\\, dx'

Series Expansion#

SymPy can compute asymptotic series expansions of functions around a point. To compute the expansion of \(f(x)\) around the point \(x = x_0\) terms of order \(x^n\) use f(x).series(x,x0,n).x0 and n can be omitted, in which case the defaults x0=0 and n=6 will be used.

expr = exp(sin(x))
expr.series(x, 0, 4)
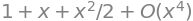
../../_images/SymPy_47_0.png

The \(O\left(x^4\right)\) term at the end represents the Landau order term at x=0 (not to be confused with big O notation used in computer science, which generally represents the Landau order term at \(x=\infty\). All x terms with power greater than or equal to \(x^4\) are omitted. Order terms can be created and manipulated outside of series. They automatically absorb higher-order terms.

Lambdafy#

Lambdafy allows you to use SymPy expressions as functions

The easiest way to convert a SymPy expression to an expression that can be numerically evaluated is to use the lambdify function. lambdify acts like a lambda function, except it converts the SymPy names to the names of the given numerical library, usually NumPy. For example

Recall Lambda functions are just small anonymous functions

import numpy as np

x = lambda a: a + 10
print(x(np.arange(10)))

[10 11 12 13 14 15 16 17 18 19]

x = lambda a, b: a * b
print(x(5, 6))

30

def myfunc(n):
    return lambda a: a * n


mytripler = myfunc(3)

print(mytripler(11))

33

Using Lambdafy with SymPy#

x = symbols("x")
a = np.arange(10)
expr = sin(x)


f = lambdify(x, expr)

f(a)

array([ 0.        ,  0.84147098,  0.90929743,  0.14112001, -0.7568025 ,
       -0.95892427, -0.2794155 ,  0.6569866 ,  0.98935825,  0.41211849])