import matplotlib.pyplot as plt
import numpy as np
import pandas as pd


from sklearn.datasets import make_blobs, load_breast_cancer
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix, classification_report

Support Vector Machines#

A type of discriminate machine learning model

They try and build a plane in space that separates examples that belong to different classes with the widest possible margin

New examples that are mapped onto that space get “classified” based on which side of the boundary they fall on

Example: Random Data#

# creating datasets X containing n_samples 
# Y containing two classes 
X, Y = make_blobs(n_samples=500, centers=2, 
                  random_state=0, cluster_std=0.40) 
  
# plotting scatters  
plt.scatter(X[:, 0], X[:, 1], c=Y, s=50, cmap='RdBu'); 
plt.show()  

../_images/Support_Vector_Machines_6_0.png

In this case, it is very easy to classify the points with a linear boundary

# creating line space between -1 to 3.5  
xfit = np.linspace(-1, 3.5) 
  
# plotting scatter 
plt.scatter(X[:, 0], X[:, 1], c=Y, s=50, cmap='RdBu') 
  
# plot a line between the different sets of data 
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]: 
    yfit = m * xfit + b 
    plt.plot(xfit, yfit, '-k') 
    plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',  
    color='#AAAAAA', alpha=0.4) 
  
plt.xlim(-1, 3.5); 
plt.show() 

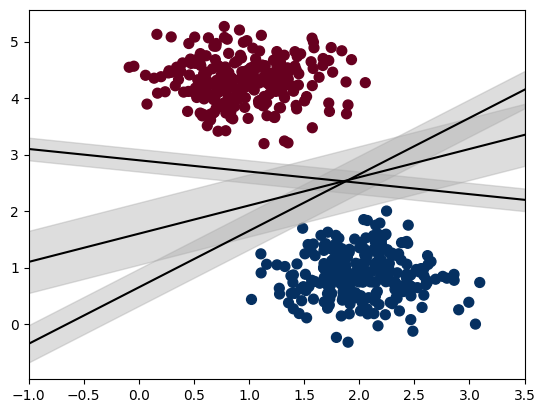
../_images/Support_Vector_Machines_8_0.png

SVMs try and find the widest possible perpendicular distance between the dividing vector and the points

Example: Breast Cancer Data#

Step 1: Load the Data#

We’ll use the built-in breast cancer dataset from Scikit-Learn. We can get with the load function:

cancer = load_breast_cancer()

Step 2: Understanding the Data#

The data set is presented in a dictionary form:

cancer.keys()

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

The DESCR contains a description of the information in the dataset

print(cancer['DESCR'])

.. _breast_cancer_dataset:

Breast cancer wisconsin (diagnostic) dataset
--------------------------------------------

**Data Set Characteristics:**

    :Number of Instances: 569

    :Number of Attributes: 30 numeric, predictive attributes and the class

    :Attribute Information:
        - radius (mean of distances from center to points on the perimeter)
        - texture (standard deviation of gray-scale values)
        - perimeter
        - area
        - smoothness (local variation in radius lengths)
        - compactness (perimeter^2 / area - 1.0)
        - concavity (severity of concave portions of the contour)
        - concave points (number of concave portions of the contour)
        - symmetry
        - fractal dimension ("coastline approximation" - 1)

        The mean, standard error, and "worst" or largest (mean of the three
        worst/largest values) of these features were computed for each image,
        resulting in 30 features.  For instance, field 0 is Mean Radius, field
        10 is Radius SE, field 20 is Worst Radius.

        - class:
                - WDBC-Malignant
                - WDBC-Benign

    :Summary Statistics:

    ===================================== ====== ======
                                           Min    Max
    ===================================== ====== ======
    radius (mean):                        6.981  28.11
    texture (mean):                       9.71   39.28
    perimeter (mean):                     43.79  188.5
    area (mean):                          143.5  2501.0
    smoothness (mean):                    0.053  0.163
    compactness (mean):                   0.019  0.345
    concavity (mean):                     0.0    0.427
    concave points (mean):                0.0    0.201
    symmetry (mean):                      0.106  0.304
    fractal dimension (mean):             0.05   0.097
    radius (standard error):              0.112  2.873
    texture (standard error):             0.36   4.885
    perimeter (standard error):           0.757  21.98
    area (standard error):                6.802  542.2
    smoothness (standard error):          0.002  0.031
    compactness (standard error):         0.002  0.135
    concavity (standard error):           0.0    0.396
    concave points (standard error):      0.0    0.053
    symmetry (standard error):            0.008  0.079
    fractal dimension (standard error):   0.001  0.03
    radius (worst):                       7.93   36.04
    texture (worst):                      12.02  49.54
    perimeter (worst):                    50.41  251.2
    area (worst):                         185.2  4254.0
    smoothness (worst):                   0.071  0.223
    compactness (worst):                  0.027  1.058
    concavity (worst):                    0.0    1.252
    concave points (worst):               0.0    0.291
    symmetry (worst):                     0.156  0.664
    fractal dimension (worst):            0.055  0.208
    ===================================== ====== ======

    :Missing Attribute Values: None

    :Class Distribution: 212 - Malignant, 357 - Benign

    :Creator:  Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian

    :Donor: Nick Street

    :Date: November, 1995

This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.
https://goo.gl/U2Uwz2

Features are computed from a digitized image of a fine needle
aspirate (FNA) of a breast mass.  They describe
characteristics of the cell nuclei present in the image.

Separating plane described above was obtained using
Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree
Construction Via Linear Programming." Proceedings of the 4th
Midwest Artificial Intelligence and Cognitive Science Society,
pp. 97-101, 1992], a classification method which uses linear
programming to construct a decision tree.  Relevant features
were selected using an exhaustive search in the space of 1-4
features and 1-3 separating planes.

The actual linear program used to obtain the separating plane
in the 3-dimensional space is that described in:
[K. P. Bennett and O. L. Mangasarian: "Robust Linear
Programming Discrimination of Two Linearly Inseparable Sets",
Optimization Methods and Software 1, 1992, 23-34].

This database is also available through the UW CS ftp server:

ftp ftp.cs.wisc.edu
cd math-prog/cpo-dataset/machine-learn/WDBC/

.. topic:: References

   - W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction 
     for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on 
     Electronic Imaging: Science and Technology, volume 1905, pages 861-870,
     San Jose, CA, 1993.
   - O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and 
     prognosis via linear programming. Operations Research, 43(4), pages 570-577, 
     July-August 1995.
   - W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
     to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994) 
     163-171.

# A list of the feature names
cancer['feature_names']

array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
       'mean smoothness', 'mean compactness', 'mean concavity',
       'mean concave points', 'mean symmetry', 'mean fractal dimension',
       'radius error', 'texture error', 'perimeter error', 'area error',
       'smoothness error', 'compactness error', 'concavity error',
       'concave points error', 'symmetry error',
       'fractal dimension error', 'worst radius', 'worst texture',
       'worst perimeter', 'worst area', 'worst smoothness',
       'worst compactness', 'worst concavity', 'worst concave points',
       'worst symmetry', 'worst fractal dimension'], dtype='<U23')

Step 3: Building the Data Structure for Training#

df_feat = pd.DataFrame(cancer['data'],columns=cancer['feature_names'])
df_feat.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 569 entries, 0 to 568
Data columns (total 30 columns):
 #   Column                   Non-Null Count  Dtype  
---  ------                   --------------  -----  
 mean radius              569 non-null    float64
 mean texture             569 non-null    float64
 mean perimeter           569 non-null    float64
 mean area                569 non-null    float64
 mean smoothness          569 non-null    float64
 mean compactness         569 non-null    float64
 mean concavity           569 non-null    float64
 mean concave points      569 non-null    float64
 mean symmetry            569 non-null    float64
 mean fractal dimension   569 non-null    float64
radius error             569 non-null    float64
texture error            569 non-null    float64
perimeter error          569 non-null    float64
area error               569 non-null    float64
smoothness error         569 non-null    float64
compactness error        569 non-null    float64
concavity error          569 non-null    float64
concave points error     569 non-null    float64
symmetry error           569 non-null    float64
fractal dimension error  569 non-null    float64
worst radius             569 non-null    float64
worst texture            569 non-null    float64
worst perimeter          569 non-null    float64
worst area               569 non-null    float64
worst smoothness         569 non-null    float64
worst compactness        569 non-null    float64
worst concavity          569 non-null    float64
worst concave points     569 non-null    float64
worst symmetry           569 non-null    float64
worst fractal dimension  569 non-null    float64
dtypes: float64(30)
memory usage: 133.5 KB

# Views how the labels are structured
cancer['target']

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
       0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0,
       1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0,
       1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1,
       1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0,
       0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1,
       1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0,
       0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0,
       1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1,
       1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0,
       0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0,
       0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0,
       1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1,
       1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1,
       1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0,
       1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1,
       1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1,
       1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1])

df_target = pd.DataFrame(cancer['target'],columns=['Cancer'])

Step 4: Validate the Data Structure#

df_feat.head()

	mean radius	mean texture	mean perimeter	mean area	mean smoothness	mean compactness	mean concavity	mean concave points	mean symmetry	mean fractal dimension	...	worst radius	worst texture	worst perimeter	worst area	worst smoothness	worst compactness	worst concavity	worst concave points	worst symmetry	worst fractal dimension
0	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.3001	0.14710	0.2419	0.07871	...	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890
1	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.0869	0.07017	0.1812	0.05667	...	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902
2	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.1974	0.12790	0.2069	0.05999	...	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758
3	11.42	20.38	77.58	386.1	0.14250	0.28390	0.2414	0.10520	0.2597	0.09744	...	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300
4	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.1980	0.10430	0.1809	0.05883	...	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678

5 rows × 30 columns

Generally, at this stage, one would visualize that data using domain knowledge

Step 5: Test-Train Split#

X_train, X_test, y_train, y_test = train_test_split(df_feat, np.ravel(df_target), test_size=0.30, random_state=101)

Step 6: Train the Model#

model = SVC(gamma='auto')
model.fit(X_train,y_train)

SVC(gamma='auto')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

X_train

	mean radius	mean texture	mean perimeter	mean area	mean smoothness	mean compactness	mean concavity	mean concave points	mean symmetry	mean fractal dimension	...	worst radius	worst texture	worst perimeter	worst area	worst smoothness	worst compactness	worst concavity	worst concave points	worst symmetry	worst fractal dimension
178	13.010	22.22	82.01	526.4	0.06251	0.01938	0.001595	0.001852	0.1395	0.05234	...	14.00	29.02	88.18	608.8	0.08125	0.03432	0.007977	0.009259	0.2295	0.05843
421	14.690	13.98	98.22	656.1	0.10310	0.18360	0.145000	0.063000	0.2086	0.07406	...	16.46	18.34	114.10	809.2	0.13120	0.36350	0.321900	0.110800	0.2827	0.09208
57	14.710	21.59	95.55	656.9	0.11370	0.13650	0.129300	0.081230	0.2027	0.06758	...	17.87	30.70	115.70	985.5	0.13680	0.42900	0.358700	0.183400	0.3698	0.10940
514	15.050	19.07	97.26	701.9	0.09215	0.08597	0.074860	0.043350	0.1561	0.05915	...	17.58	28.06	113.80	967.0	0.12460	0.21010	0.286600	0.112000	0.2282	0.06954
548	9.683	19.34	61.05	285.7	0.08491	0.05030	0.023370	0.009615	0.1580	0.06235	...	10.93	25.59	69.10	364.2	0.11990	0.09546	0.093500	0.038460	0.2552	0.07920
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
552	12.770	29.43	81.35	507.9	0.08276	0.04234	0.019970	0.014990	0.1539	0.05637	...	13.87	36.00	88.10	594.7	0.12340	0.10640	0.086530	0.064980	0.2407	0.06484
393	21.610	22.28	144.40	1407.0	0.11670	0.20870	0.281000	0.156200	0.2162	0.06606	...	26.23	28.74	172.00	2081.0	0.15020	0.57170	0.705300	0.242200	0.3828	0.10070
75	16.070	19.65	104.10	817.7	0.09168	0.08424	0.097690	0.066380	0.1798	0.05391	...	19.77	24.56	128.80	1223.0	0.15000	0.20450	0.282900	0.152000	0.2650	0.06387
337	18.770	21.43	122.90	1092.0	0.09116	0.14020	0.106000	0.060900	0.1953	0.06083	...	24.54	34.37	161.10	1873.0	0.14980	0.48270	0.463400	0.204800	0.3679	0.09870
523	13.710	18.68	88.73	571.0	0.09916	0.10700	0.053850	0.037830	0.1714	0.06843	...	15.11	25.63	99.43	701.9	0.14250	0.25660	0.193500	0.128400	0.2849	0.09031

398 rows × 30 columns

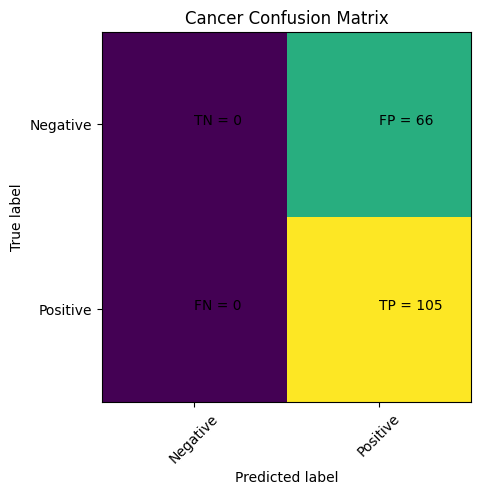
Step 7: Visualize the Results#

predictions = model.predict(X_test)
cm = confusion_matrix(y_test,predictions)

plt.clf()
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.viridis)
classNames = ['Negative','Positive']
plt.title('Cancer Confusion Matrix')
plt.ylabel('True label')
plt.xlabel('Predicted label')
tick_marks = np.arange(len(classNames))
plt.xticks(tick_marks, classNames, rotation=45)
plt.yticks(tick_marks, classNames)
s = [['TN','FP'], ['FN', 'TP']]
for i in range(2):
    for j in range(2):
        plt.text(j,i, str(s[i][j])+" = "+str(cm[i][j]))
plt.show()

../_images/Support_Vector_Machines_31_0.png

print(classification_report(y_test,predictions))

              precision    recall  f1-score   support

           0       0.00      0.00      0.00        66
           1       0.61      1.00      0.76       105

    accuracy                           0.61       171
   macro avg       0.31      0.50      0.38       171
weighted avg       0.38      0.61      0.47       171

C:\Users\jca92\.conda\envs\jupyterbook\lib\site-packages\sklearn\metrics\_classification.py:1334: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
  _warn_prf(average, modifier, msg_start, len(result))
C:\Users\jca92\.conda\envs\jupyterbook\lib\site-packages\sklearn\metrics\_classification.py:1334: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
  _warn_prf(average, modifier, msg_start, len(result))
C:\Users\jca92\.conda\envs\jupyterbook\lib\site-packages\sklearn\metrics\_classification.py:1334: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
  _warn_prf(average, modifier, msg_start, len(result))

This is not good … Our Machine Thinks Everyone has Cancer!!!!

What did we do wrong?

Step 4a: Scaling the Data#

When models fail:

Check how the data was normalized
Optimize the model parameters

df_feat.head()

	mean radius	mean texture	mean perimeter	mean area	mean smoothness	mean compactness	mean concavity	mean concave points	mean symmetry	mean fractal dimension	...	worst radius	worst texture	worst perimeter	worst area	worst smoothness	worst compactness	worst concavity	worst concave points	worst symmetry	worst fractal dimension
0	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.3001	0.14710	0.2419	0.07871	...	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890
1	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.0869	0.07017	0.1812	0.05667	...	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902
2	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.1974	0.12790	0.2069	0.05999	...	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758
3	11.42	20.38	77.58	386.1	0.14250	0.28390	0.2414	0.10520	0.2597	0.09744	...	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300
4	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.1980	0.10430	0.1809	0.05883	...	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678

5 rows × 30 columns

The features have vastly different scales which makes them weighted unequally

Standard Scaler#

Removes the mean and scales to a unit variance

\[ z = \frac{x - \mu}{\sigma}\]

\(\mu\) is the mean
\(\sigma\) is the standard deviation

The result is all features will have a mean of 0 and a variance of 1

# It is usually a good idea to scale the data for SVM training.
# We are cheating a bit in this example in scaling all of the data,
# instead of fitting the transformation on the training set and
# just applying it on the test set.


scaler = StandardScaler()
df_feat = scaler.fit_transform(df_feat)
df_feat = pd.DataFrame(df_feat,columns=cancer['feature_names'])

df_feat.head()

	mean radius	mean texture	mean perimeter	mean area	mean smoothness	mean compactness	mean concavity	mean concave points	mean symmetry	mean fractal dimension	...	worst radius	worst texture	worst perimeter	worst area	worst smoothness	worst compactness	worst concavity	worst concave points	worst symmetry	worst fractal dimension
0	1.097064	-2.073335	1.269934	0.984375	1.568466	3.283515	2.652874	2.532475	2.217515	2.255747	...	1.886690	-1.359293	2.303601	2.001237	1.307686	2.616665	2.109526	2.296076	2.750622	1.937015
1	1.829821	-0.353632	1.685955	1.908708	-0.826962	-0.487072	-0.023846	0.548144	0.001392	-0.868652	...	1.805927	-0.369203	1.535126	1.890489	-0.375612	-0.430444	-0.146749	1.087084	-0.243890	0.281190
2	1.579888	0.456187	1.566503	1.558884	0.942210	1.052926	1.363478	2.037231	0.939685	-0.398008	...	1.511870	-0.023974	1.347475	1.456285	0.527407	1.082932	0.854974	1.955000	1.152255	0.201391
3	-0.768909	0.253732	-0.592687	-0.764464	3.283553	3.402909	1.915897	1.451707	2.867383	4.910919	...	-0.281464	0.133984	-0.249939	-0.550021	3.394275	3.893397	1.989588	2.175786	6.046041	4.935010
4	1.750297	-1.151816	1.776573	1.826229	0.280372	0.539340	1.371011	1.428493	-0.009560	-0.562450	...	1.298575	-1.466770	1.338539	1.220724	0.220556	-0.313395	0.613179	0.729259	-0.868353	-0.397100

5 rows × 30 columns

Step 5: Test-Train Split#

X_train, X_test, y_train, y_test = train_test_split(df_feat, np.ravel(df_target), test_size=0.30, random_state=101)

Step 6: Train the Model#

model = SVC(gamma='auto')
model.fit(X_train,y_train)

SVC(gamma='auto')

Step 7: Visualize the Results#

predictions = model.predict(X_test)
cm = confusion_matrix(y_test,predictions)

plt.clf()
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.viridis)
classNames = ['Negative','Positive']
plt.title('Cancer Confusion Matrix')
plt.ylabel('True label')
plt.xlabel('Predicted label')
tick_marks = np.arange(len(classNames))
plt.xticks(tick_marks, classNames, rotation=45)
plt.yticks(tick_marks, classNames)
s = [['TN','FP'], ['FN', 'TP']]
for i in range(2):
    for j in range(2):
        plt.text(j,i, str(s[i][j])+" = "+str(cm[i][j]))
plt.show()

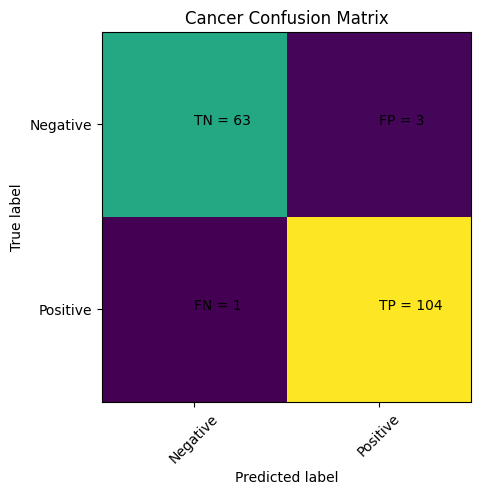
../_images/Support_Vector_Machines_47_0.png

That looks way better

MEM T680: Fall 2022: Data Analysis and Machine Learning

Support Vector Machines

Contents

Support Vector Machines#

Example: Random Data#

Example: Breast Cancer Data#

Step 1: Load the Data#

Step 2: Understanding the Data#

Step 3: Building the Data Structure for Training#

Step 4: Validate the Data Structure#

Step 5: Test-Train Split#

Step 6: Train the Model#

Step 7: Visualize the Results#

Step 4a: Scaling the Data#

Standard Scaler#

Step 5: Test-Train Split#

Step 6: Train the Model#

Step 7: Visualize the Results#