🧪🖥️ Lab 8: Pollutant Triangulation
=======🧪🖥 Lab 8: Pollutant Triangulation
>>>>>>> Stashed changesContents
%%capture
# OTTER IGNORE
! pip install drexel-jupyter-logger
! pip install otter-grader
=======
# Initialize Otter
import otter
grader = otter.Notebook("lab8-pollutant.ipynb")
>>>>>>> Stashed changes
# Initialize Otter
import otter
grader = otter.Notebook("lab8-pollutant.ipynb")
=======
🧪🖥 Lab 8: Pollutant Triangulation#
This lab uses classes to solve a problem involving pollutant triangulation.
%%capture
# OTTER IGNORE
! pip install drexel-jupyter-logger
>>>>>>> Stashed changes
<<<<<<< Updated upstream
🧪🖥️ Lab 8: Pollutant Triangulation#
This lab uses classes to solve a problem involving pollutant triangulation.
=======
>>>>>>> Stashed changes
import drexel_jupyter_logger
import matplotlib.pyplot as plt
import numpy as np
# import IPython.display as ipd
Use triangulation to locate pollutant source#
Triangulation, such as used in GPS positioning uses three points and two distances to calculate the location of an unknown point.
Now, let’s suppose that the unknown point is actually a point source for some pollutant X, and at time 0 it
releases a burst of Chemical X. Assume no wind, and that X diffuses freely from its release point.
<<<<<<< Updated upstream
Suppose that we have measurement devices at the three points 1, 2, and 3 that track the concentration of X as a function of time, and that the concentration of X is detected to peak at times \(t_1\), \(t_2\), and \(t_3\), at each point, respectively. Can we determine the location of the pollutant point source?
=======
Suppose that we have measurement devices at the three points 1, 2, and 3 that track the concentration of X as a function of time, and that the concentration of X is detected to peak at times \(t_1\), \(t_2\), and \(t_3\), at each point, respectively. Can we determine the location of the evil point source?
>>>>>>> Stashed changes
Task 1: Make a class for point in pollutant system#
In this system, we have collected data at points \((x_1,y_1)\), \((x_2,y_2)\), and \((x_3,y_3)\), at times \(t_1\), \(t_2\), and \(t_3\) respectively. We would like to encapsulate this data, and find a way to extract distance using the diffusivity of \(X\) \((D_X)\).
Let’s make the assumption that the time intervals \((t_i)\) scale with the square of the distance \((d_i)\) divided by the diffusivity of \(X\) \((D_X)\):
\[ t_i ~ \frac{d_i^2}{D_X} \]
We can express the diffusivity using the following diffusion constant:
\[ K = \sqrt{D_X} \]
<<<<<<< Updated upstream
That satisfies the conditions
\[ d_1 = K\sqrt{t_1} \]
\[ d_2 = K\sqrt{t_2} \]
\[ d_3 = K\sqrt{t_3} \]
=======
That satisfies the conditions
$\( d_1 = K\sqrt{t_1} \)\(
\)\( d_2 = K\sqrt{t_2} \)\(
\)\( d_3 = K\sqrt{t_3} \)$
>>>>>>> Stashed changes
Write python code to do the following:
Define a class called Point
Define the class constructor to accept as argument the floats x,y,t, in that order. Make sure your parameters are in the right order! Store each value in a data member, so that they can be used in other methods.
Define a method called diffusion_distance which accepts as input the constant K, and returns the distance calculated using the Point member self.t.
Your code replaces the prompt: ...
...
# Create point objects P1, P2, P3
Pt1 = Point(0,1,1)
Pt2 = Point(1,0,2)
Pt3 = Point(2,3,2)
print(f'Members of P1: ({Pt1.x},{Pt1.y},{Pt1.t})')
# Solve diffusion distance
dist1 = Pt1.diffusion_distance(2.5)
print('Calculate diffusion distance of P1:', dist1)
# Plot P1,P2,P3
plt.clf()
plt.plot(Pt1.x,Pt1.y,'ro')
plt.plot(Pt2.x,Pt2.y,'b*')
plt.plot(Pt3.x,Pt3.y,'k+')
plt.grid()
grader.check("task1-Point-class")
Task 2: Make a class to triangulate between 3 points#
In the previous task, we determined how to calculate the distance between a point and a pollutant source, given diffusion constant \(K\) and time \(t\). How can we use this information to find the location of a pollutant source?
Intro to Triangulation
Triangulation is the process of locating an unknown point given two know points, and two known distances.
Consider two points \((x_1,y_1)\) and \((x_2,y_2\)).
<<<<<<< Updated upstream
Let \((x,y)\) be an unknown point whose respective distances to the two points, \(d_1\) and \(d_2\), are known. The Pythagorean theorem allows us to express \(x\) and \(y\) (the coordinates of the unknown point) in terms of \((x_1,y_1)\), \((x_2,y_2)\), \(d_1\), and \(d_2\):
\[ d_1^{2} = (x - x_1)^{2} + (y - y_1)^{2}\]
\[ d_2^{2} = (x - x_2)^{2} + (y - y_2)^{2}\]
Inverting these two formulae to make them explicit in \(x\) and \(y\) is really a lot of fun, but it takes a while. Here is the final result:
\[ x_{\pm} = \frac{1}{2(1 + b^2)} \left[ 2 [x_1 - b(a - y_1)] \pm [4(b(a - y_1) - x_1)^2 - 4(1 + b^2)(x_1^{2} - d_1^{2} + (y_1 - a)^{2})]^{\frac{1}{2}} \right] \]
\[ y_{\pm} = a + bx_{\pm} \]
where
\[ a = \frac{d_1^{2} - d_2^{2} - [(x_1^{2} + y_1^{2}) - (x_2^{2} + y_2^{2})]}{2(y_2 - y_1)} \]
and
\[ b = - \frac{x_2 - x_1}{y_2 - y_1} \]
=======
Let \((x,y)\) be an unknown point whose respective distances to the two points, \(d_1\) and \(d_2\), are known. The Pythagorean theorem allows us to express \(x\) and \(y\) (the coordinates of the unknown point) in terms of \((x_1,y_1)\), \((x_2,y_2)\), \(d_1\), and \(d_2\):
$\( d_1^{2} = (x - x_1)^{2} + (y - y_1)^{2}\)\(
\)\( d_2^{2} = (x - x_2)^{2} + (y - y_2)^{2}\)$
Inverting these two formulae to make them explicit in \(x\) and \(y\) is really a lot of fun, but it takes a while. Here is the final result:
$\( x_{\pm} = \frac{1}{2(1 + b^2)} \left[ 2 [x_1 - b(a - y_1)] \pm [4(b(a - y_1) - x_1)^2 - 4(1 + b^2)(x_1^{2} - d_1^{2} + (y_1 - a)^{2})]^{\frac{1}{2}} \right] \)\(
\)\( y_{\pm} = a + bx_{\pm} \)$
where
$\( a = \frac{d_1^{2} - d_2^{2} - [(x_1^{2} + y_1^{2}) - (x_2^{2} + y_2^{2})]}{2(y_2 - y_1)} \)$
and
$\( b = - \frac{x_2 - x_1}{y_2 - y_1} \)$
>>>>>>> Stashed changes
Note that the two possible values for \(x\), \(x_+\) and \(x_-\), arise from the positive and negative sense of the square root, and the value of \(y\) derives from its particular \(x\). So because of the power of 2 in the Pythagorean theorem, we find that there are two possible points, \((x_+, y_+)\) and \((x_-, y_-)\), that are each \(d_1\) from \((x_1, y_1)\) and \(d_2\) from \((x_2, y_2)\). These are shown by the star and cross in the figure below.
“Triangulation” refers to the fact that we need a third known point to decide which of \((x_+, y_+)\) and \((x_-, y_-)\) is our sought-after point. We would like the final unknown point to be the one that is closer to \((x_3, y_3)\), shown as the star in the figure below:
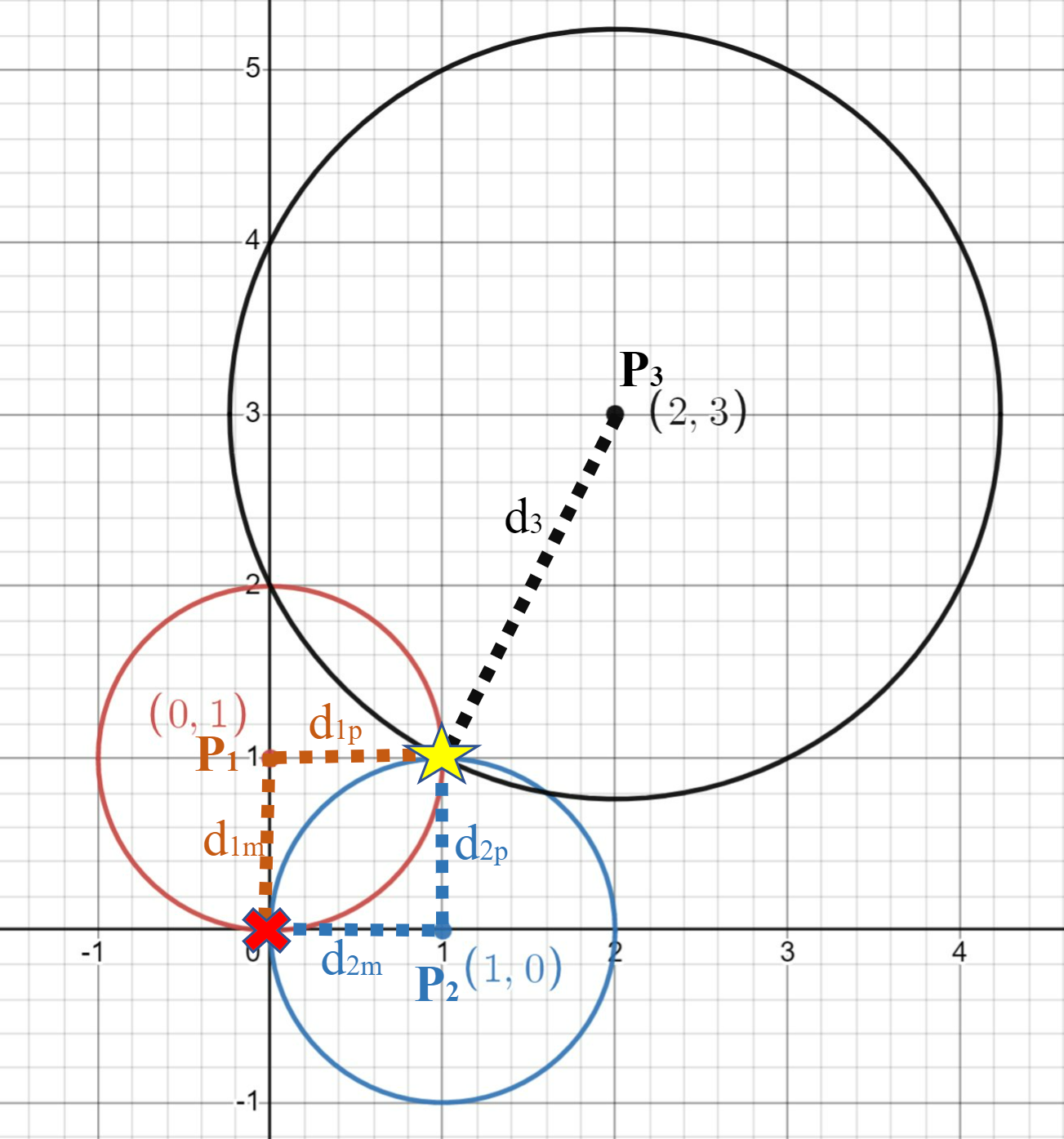
Write a python code to do the following:
Create a class Point_System
Define the class constructor to accept as argument the Point objects P1,P2, and P3, in that order. Store each value in a data member, so that they can be used in other methods.
Define a method called pythagoras which accepts as input and x1,y1,x2,y2. This method should return the euclidean distance between the two points.
Define a method called a_b which accepts as input the distances between a point and self.P1 and self.P2, as d1 and d2 respectively. This method should return the tuple a,b, calculated with the equation above.
Define a method called x_y which accepts as input the distances between a point and self.P1 and self.P2, as d1 and d2 respectively. This method should return the tuple xm,ym,xp,yp, which are the “minus” coordinates (xm,ym) and “plus” coordinates (xp,yp) of a point, calculated with the equation above.
Define a method called pythagoras which accepts as input and x1,y1,x2,y2, which are the coordinates of the points self.P1 and self.P2. This method should return the euclidean distance between the two points.
Define a method called a_b which accepts as input the distances between a point and self.P1 and self.P2, as d1 and d2 respectively. This method should return the tuple a,b, calculated with the equation above.
Define a method called x_y which accepts as input the distances between a point and self.P1 and self.P2, as d1 and d2 respectively. This method should return the tuple m,ym,xp,yp, which are the “minus” coordinates (xm,ym) and “plus” coordinates (xp,yp) of a point, calculated with the equation above.
Define a method called triangulate which accepts as input the distances between a point and self.P1 and self.P2, as d1 and d2 respectively. This method should return the tuple xf,yf, the coordinate closest to the third point, self.P3.
Calculate the potential coordinates of a point the distance d1 from point self.P1, and distance d2 from self.P2 using the method we defined, x_y. Assign this to the variables xm,ym,xp,yp.
Assign a variable d3m to be the distance between the estimated “minus” coordinate xm,ym and the point self.P3
Assign a variable d3p to be the distance between the estimated “plus” coordinate xp,yp and the point self.P3
Check whether d3m or d3p is smaller. Set the corresponding \((x,y)\) coordinates to variables xf,yf
Return the final triangulated coordinates, xf,yf.
Your code replaces the prompt: ...
...
# create Point object P1, P2, P3
Pt1 = Point(0,1,1)
Pt2 = Point(1,0,2)
Pt3 = Point(2,3,2)
# Create Point_System object System, using P1, P2, P3 as inputs
System = Point_System(Pt1,Pt2,Pt3)
# Plot points Point_System objects P1, P2, P3
plt.clf()
plt.plot(System.P1.x,System.P1.y,'ro')
plt.plot(System.P2.x,System.P2.y,'b*')
plt.plot(System.P3.x,System.P3.y,'k+')
plt.grid()
grader.check("task2-System-class")
Task 3: Predict location of pollutant and diffusivity#
Our system consists of three points, \(P_1=(-4,7), P_2=(-5,-6), P_3=(9,1)\), and a pollution source with unknown coordinates and diffusion coefficient \(K\). After the release of the chemical, the pollution peaked at the three points at times \(300,400,500\) respectively. We want to estimate \(K\) and the coordinates of the pollutant.
We can achieve this using an iterative process that slowly modifies K by multiplying it by a change factor \(\epsilon\), and recalculates the predicted coordinates. The process will repeat until K is modified by less than a factor of \(10^{-6}\) (In other words, the code runs if \(|K-K\epsilon|>K10^{-6}\)). Write a code to do the following:
Create Point objects P1, P2 and P3, initialized with the coordinates and times given above
Create a Point_System object Sys initialized with point objects P1, P2 and P3.
We are satisfied with our guess when K changes by less than a factor of \(10^{-6}\) per iteration. Assign this value to variable criteria. This variable will not change!
Assign 1.0 as our initial guess of K
Assign criteria \(10^{-6}\) as our initial change factor, epsilon
Write a loop that runs until K is modified by less than a factor of \(10^{-6}\). Inside, the loop performs the following steps:
Compute the distances of d1, d2, and d3 with the given values of K.
Use triangulation to find the points xf,yf, which are the correct distance from P1 and P2, and closest to P3.
Compute the distance d3_, which is the distance between (xf,yf) and P3.
Calculate our change factor epsilon using the following equation: \(\epsilon=\sqrt{d_{3\ guess}/d_{3\ true}}\).
print the values of d3_, d3, epsilon, and K.
Change \(K\) to \(K\epsilon\).
Your code replaces the prompt: ...
# Define Variables
...
# create loop that modifies K
...
# Print the estimated diffusivity
print(f'Diffusivity of X is about {K**2:.3f}')
# Print the estimated location of the point source
<<<<<<< Updated upstream
print(f'Pollutant point source is ({xf:.3f},{yf:.3f})')
=======
print(f'Evil point source is ({xf:.3f},{yf:.3f})')
>>>>>>> Stashed changes
grader.check("task3-predict")
Take a look at the points and the pollutant source
import matplotlib.pyplot as plt
plt.clf()
plt.xlim([min([P1.x,P2.x,P3.x,xf])-1,max([P1.x,P2.x,P3.x,xf])+1])
plt.ylim([min([P1.y,P2.y,P3.y,yf])-1,max([P1.y,P2.y,P3.y,yf])+1])
plt.plot(P1.x,P1.y,'bo')
plt.plot(P2.x,P2.y,'go')
plt.plot(P3.x,P3.y,'co')
plt.plot(xf,yf,'ro')
plt.plot([P1.x,xf],[P1.y,yf],'k-')
plt.plot([P2.x,xf],[P2.y,yf],'k-')
plt.plot([P3.x,xf],[P3.y,yf],'k-')
plt.annotate('P1',xy=(P1.x,P1.y))
plt.annotate('P2',xy=(P2.x,P2.y))
plt.annotate('P3',xy=(P3.x,P3.y))
<<<<<<< Updated upstream
plt.annotate('pollutant point source',xy=(xf,yf))
=======
plt.annotate('evil point source',xy=(xf,yf))
>>>>>>> Stashed changes
plt.show()



