📝 🤖🔌 Welcome to Boolean Logic in Engineering!

Boolean Logic

🔧 Booleans in Engineering Applications

Booleans are foundational to engineering systems:

• Designing control systems (e.g., thermostats, elevators)

• Writing algorithms for robotics

• Ensuring error-checking in software systems

• Building decision-making logic in hardware circuits

🧐 What Are Booleans?

Booleans represent true or false states, like the binary language of computers:

• True and False are Python’s Boolean values.

• Ideal for representing logical states in engineering designs.

🤔 Why Booleans Matter in Engineering?

Boolean logic helps engineers:

• Simulate conditions (e.g., if a motor overheats)

• Make decisions (e.g., activate emergency protocols)

• Optimize resource allocation (e.g., power systems switching)

• Validate inputs and outputs in simulations

🛠 Boolean Basics

In Python, Booleans are straightforward:

is_operational = True
is_overheated = False

Booleans also arise from logical comparisons:

temperature = 85
is_overheated = temperature > 80

temperature = 85
is_operational = True
is_overheated = temperature > 80
print("Is operational:", is_operational)
print("Is overheated:", is_overheated)

Is operational: True
Is overheated: True

🔍 Logical Operators

Combine and manipulate Boolean values with logical operators:

• and: True if both conditions are True.

• or: True if at least one condition is True.

• not: Reverses a Boolean value.

motor_running = True
temperature_safe = False

# Check if the motor should shut down
should_shut_down = motor_running and not temperature_safe
print("Should shut down:", should_shut_down)

Should shut down: True

🎯 Real-World Example: Control Systems

Engineering systems often rely on Boolean logic:

Elevator Control

is_door_closed = True
is_weight_limit_exceeded = False
can_move = is_door_closed and not is_weight_limit_exceeded

Try it out:

is_door_closed = True
is_weight_limit_exceeded = False
can_move = is_door_closed and not is_weight_limit_exceeded
print("Can the elevator move:", can_move)

Can the elevator move: True

🧠 Boolean Comparisons

Compare values to generate Boolean results:

• Equality: ==

• Inequality: !=

• Greater/Less than: >, <, >=, <=

sensor_value = 75
threshold = 80

# Check if the sensor value is within limits
is_within_limits = sensor_value <= threshold
print("Sensor within limits:", is_within_limits)

Sensor within limits: True

🔀 Boolean Combinations in Simulations

Simulations often use multiple conditions:

has_power = True
is_safety_check_passed = True
can_operate = has_power and is_safety_check_passed

Experiment with different states:

has_power = True
is_safety_check_passed = False
can_operate = has_power and is_safety_check_passed
print("Can the system operate:", can_operate)

Can the system operate: False

📊 Equality (==) vs Identity (is)

Python provides two ways to compare objects:

• Equality (==): Checks if the values are equal.

• Identity (is): Checks if two variables point to the same object in memory.

Example:

a = [1, 2, 3]
b = [1, 2, 3]
c = a

print("a == b:", a == b)  # True, values are the same
print("a is b:", a is b)  # False, different objects in memory
print("a is c:", a is c)  # True, same object in memory

a == b: True
a is b: False
a is c: True

Discussion:

• Use == to compare contents or values (e.g., sensor readings).

• Use is to ensure two variables reference the exact same object (e.g., shared configuration data).

Engineering contexts may use is when ensuring a single control system state is shared among components.

📊 Boolean Applications in Data Processing

Booleans help filter and validate engineering data:

Example: Validating sensor readings in a CSV dataset.

readings = [100, 85, 90, 120, 70]
valid_readings = [r for r in readings if r <= 100]
print("Valid readings:", valid_readings)

Valid readings: [100, 85, 90, 70]

readings = [100, 85, 90, 120, 70]
valid_readings = [r for r in readings if r <= 100]
print("Valid readings:", valid_readings)

Valid readings: [100, 85, 90, 70]

🧮 Truth Tables for Decision-Making

Boolean logic enables decision trees and truth tables:

Input A	Input B	A AND B	A OR B
False	False	False	False
False	True	False	True
True	False	False	True
True	True	True	True

inputs = [(False, False), (False, True), (True, False), (True, True)]
for a, b in inputs:
    print(f"A: {a}, B: {b}, A AND B: {a and b}, A OR B: {a or b}")

A: False, B: False, A AND B: False, A OR B: False
A: False, B: True, A AND B: False, A OR B: True
A: True, B: False, A AND B: False, A OR B: True
A: True, B: True, A AND B: True, A OR B: True

🚀 Advanced Applications

• Fault Detection: Identify faults in industrial systems using Boolean expressions.

• Circuit Design: Simulate logic gates (AND, OR, NOT).

• Algorithm Optimization: Streamline decision-making in software and hardware.

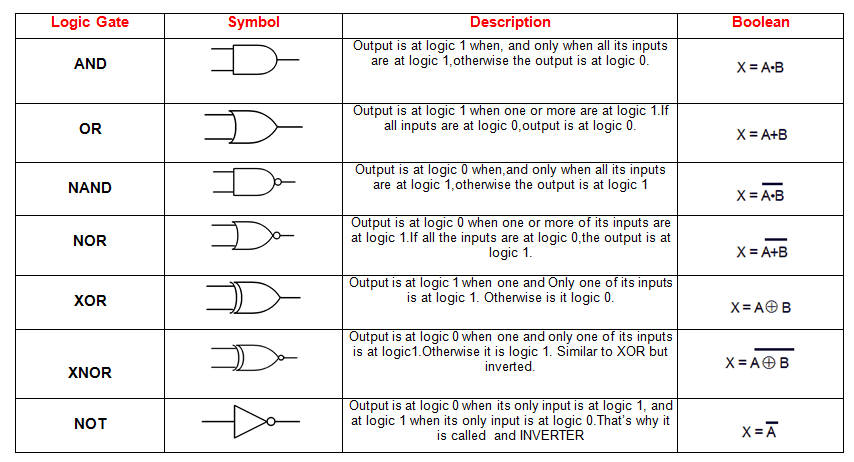
def fault_detection(sensor_a, sensor_b):
    return sensor_a or sensor_b  # True if either sensor reports a fault

print("Fault detected:", fault_detection(False, True))

Fault detected: True

🎉 Key Takeaways

• Booleans are essential for logical decision-making in engineering.

• Logical operators (and, or, not) enable complex conditions.

• Boolean logic powers control systems, data processing, and simulations.

Practice Boolean logic to build smarter systems and optimize designs!