💻 Activity: Taking Integrals with Loops

from pykubegrader.tokens.validate_token import validate_token
validate_token('type the key provided by your instructor here')

# You must make sure to run all cells in sequence using shift + enter or you might encounter errors
from pykubegrader.initialize import initialize_assignment

responses = initialize_assignment("9_loops_activity_q", "week_4", "lecture", assignment_points = 8.0, assignment_tag = 'week4-lecture')

# Initialize Otter
import otter
grader = otter.Notebook("9_loops_activity_q.ipynb")

💻 Activity: Taking Integrals with Loops#

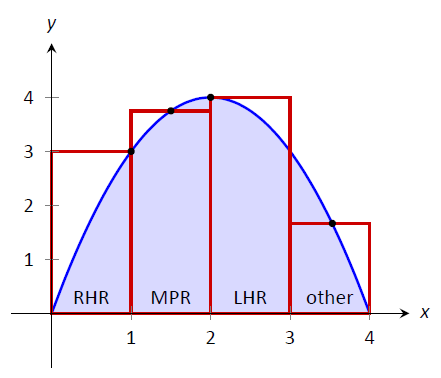
Riemann Sums

Problem Statement#

Let’s explore how two important choices impact the accuracy of this method for approximating integrals:

  1. The width of the rectangle \(h\), which is determined by the number of rectangles between \(a\) and \(b\).

  2. The value of \(x\) at which the function is evaluated (left, midpoint, or right).

Implementation#

Write a function riemann(numRectangles, evalPoint) that calculates the approximate integral of a given function using Riemann sums with the following requirements:

  1. Define the boundaries of the integral: \(a = 0\) and \(b = 5\).

  2. Use the curve \(f(x) = \sin(x/2) + 1\).

    • Create an array of \(x\) values between \(a\) and \(b\), using np.linspace(). The number of steps is determined by numRectangles.

  3. Calculate the width of each rectangle, \(h\), as: $\(h = \frac{b - a}{\text{numRectangles} - 1}\)$

  4. Initialize the variable integral_R to zero.

  5. Use a loop to calculate the integral using the value of \(f\) at the right side of each rectangle. This is if i < (numRectangles - 1).

  6. Add and assign the area of each rectangle to integral_R as: $\(\text{integral_R} += h \times f[i + 1]\)$

We have provided the necessary print statement and test statements to tests your code.

Example Usage#

Call the function using different values for numRectangles (e.g., 2, 5, and 11) and "right" as the evaluation point to compare the approximations.

import numpy as np


def riemann(numRectangles, evalPoint):
    # The function riemann takes two inputs: numRectangles and evalPoint
    # numRectangles is the number of rectangles to use in the Riemann sum

    # Define the boundaries of the integral
    ...

    # Define the curve
    x = ...
    f = ...

    # Determine the width of each rectangle
    h = ...

    # Initialize the integral
    integral_R = ...

    # Integrate using the value of f at the right
    ...

    # Print the integral, number of rectangles, and the chosen point for evaluation
    print(
        f"The integral is {integral_R:.6f} for {numRectangles} using the {evalPoint} point for evaluating the function."
    )


# Call the function with different inputs
riemann(2, "right")
riemann(5, "right")
riemann(11, "right")
riemann(51, "right")

grader.check("integrals-riemann-sums")

Submitting Assignment#

Please run the following block of code using shift + enter to submit your assignment, you should see your score.

from pykubegrader.tokens.validate_token import validate_token
validate_token()


from pykubegrader.submit.submit_assignment import submit_assignment

submit_assignment("week4-lecture", "9_loops_activity_q")